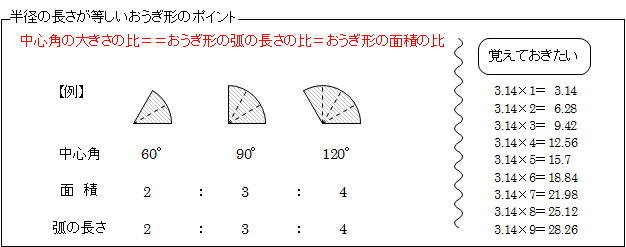
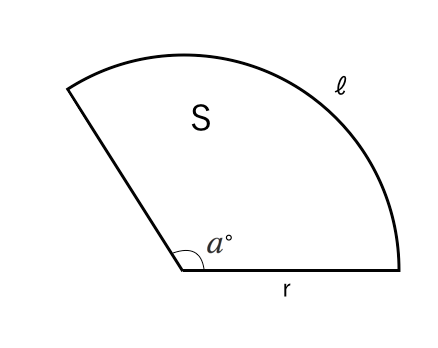
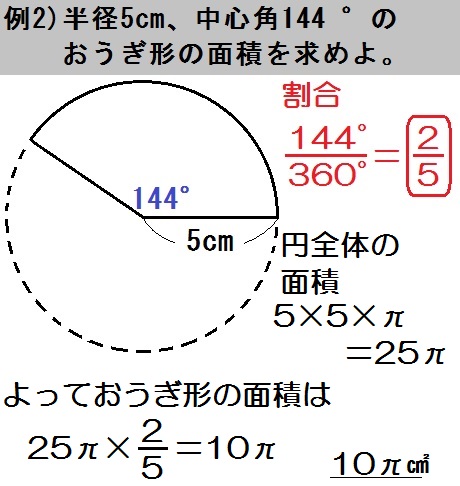
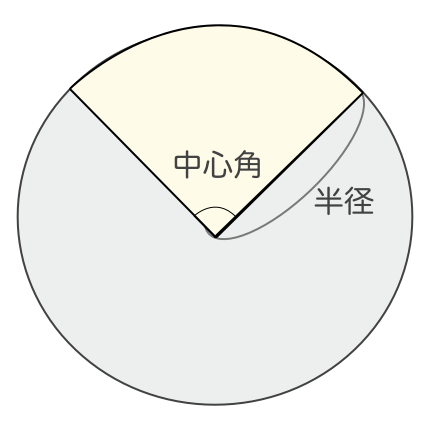
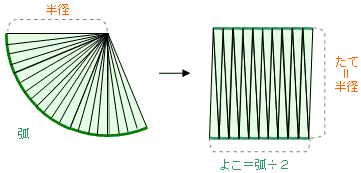
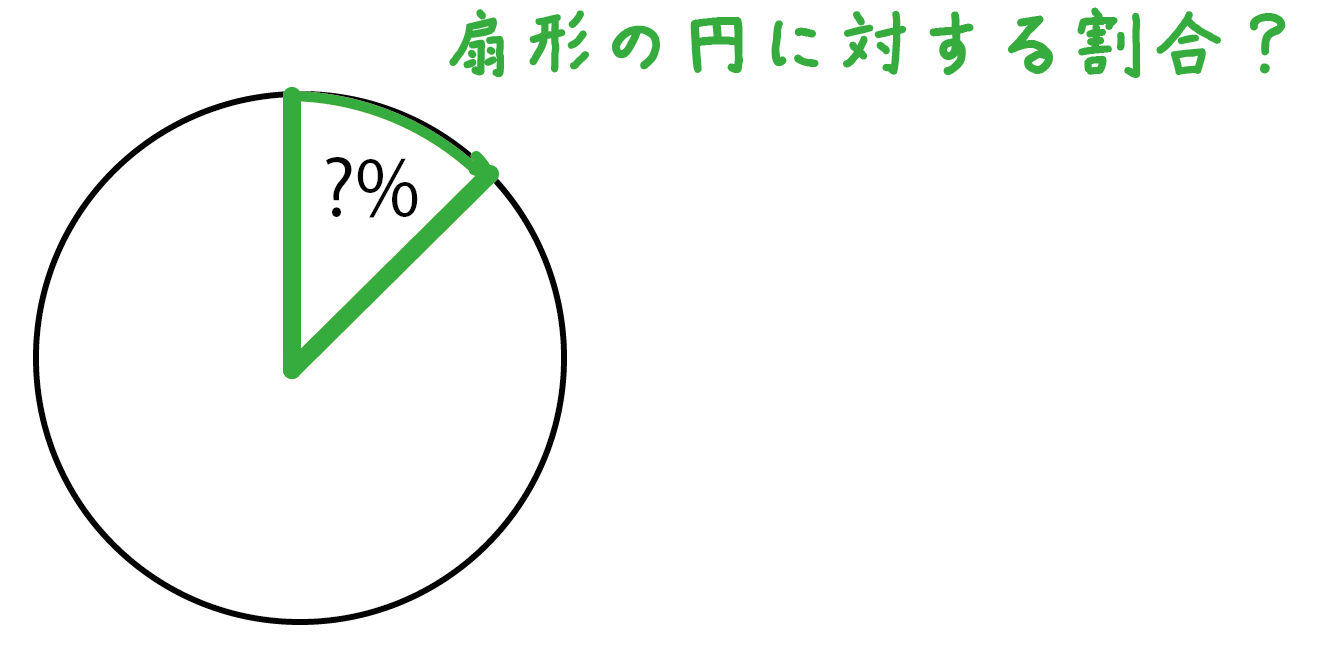
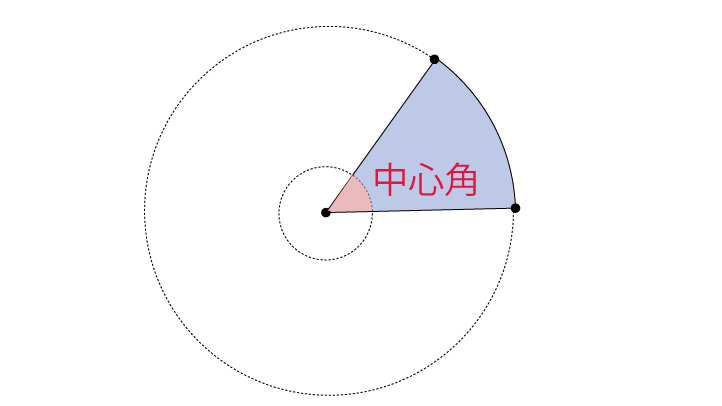
おうぎ形の面積 90度のおうぎ形をイメージすれば、おうぎ形の面積も「元の円の面積」×おうぎ形の割合と分かりますね。 ( (図)) おうぎ形の面積=半径×半径×314× 中心角 360 上の2
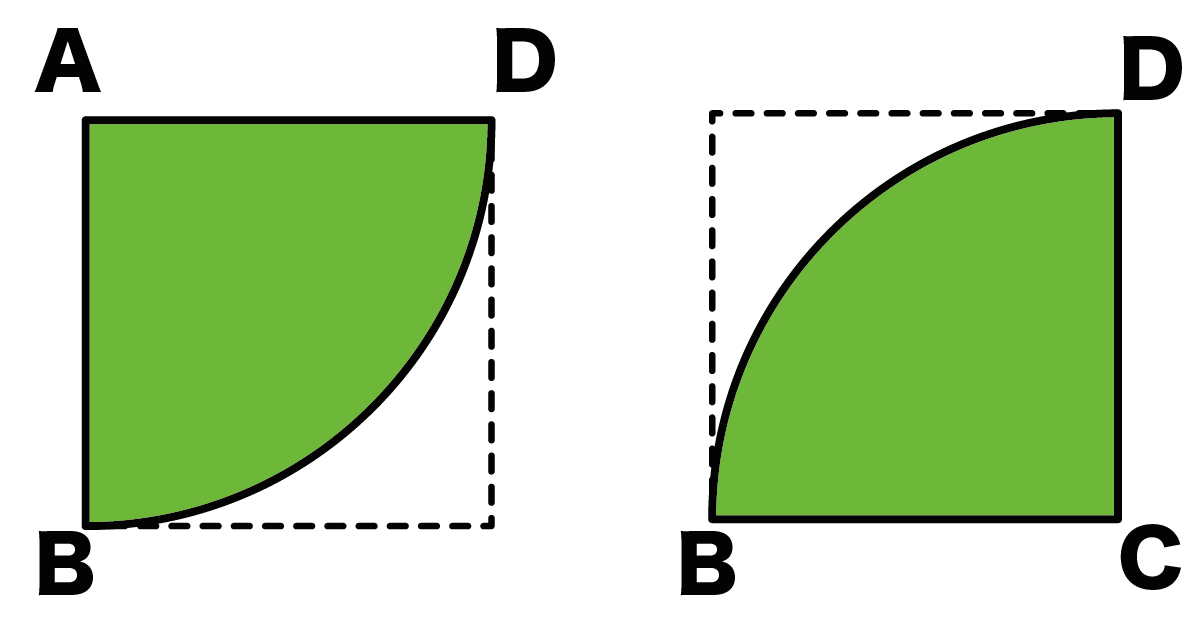
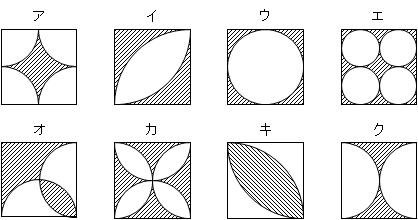
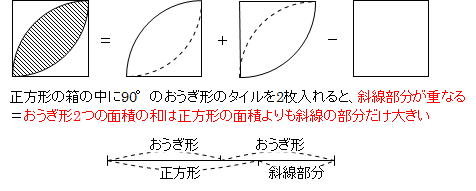
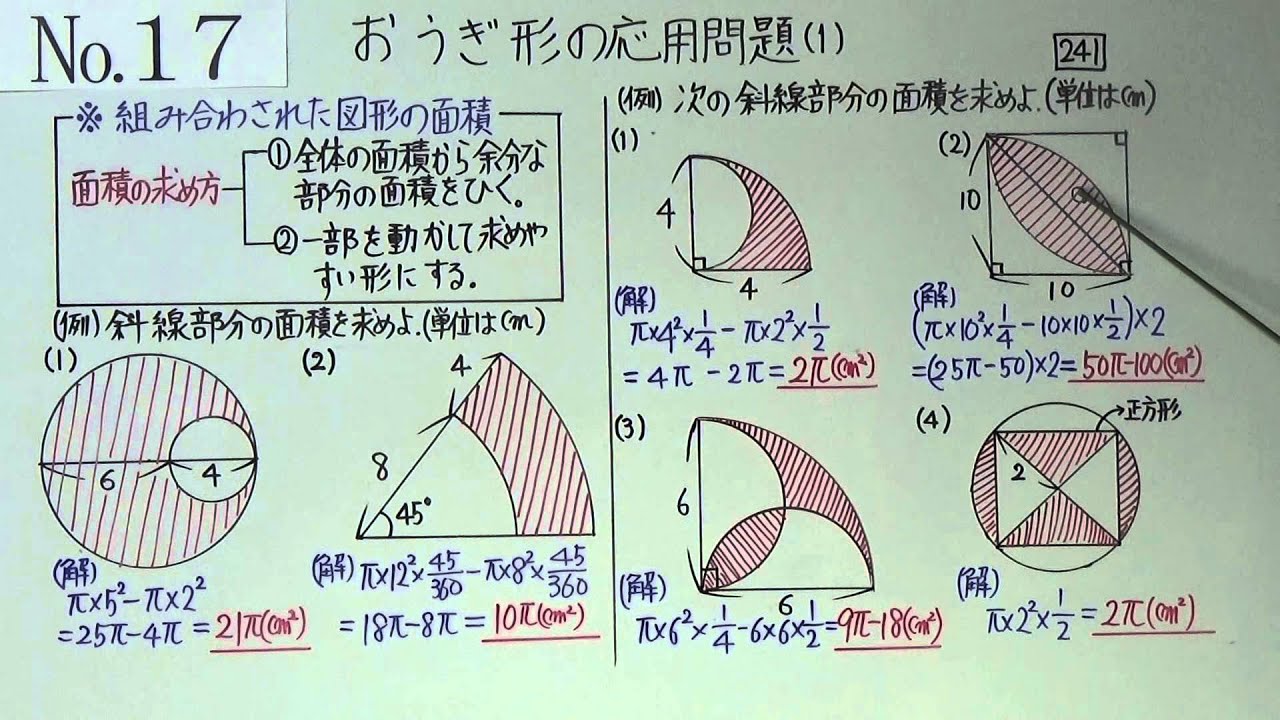
おうぎ形 面積 応用問題- イの面積は 10×10×314÷4ー50 =285 (㎠) イ÷ア 50÷285 =057 よって ア:イ=1:057 上の考え方を使うと下の正方形と色のついた部分の面積比も 1:057 になる。 正方形おうぎ形の面積 = 半径 × 半径 × π × 中心角 360° おうぎ形の弧の長さ = 直径 × π × 中心角 360° 弧の長さ5π cm,面積πcm2のおうぎ形の 半径を求めよ。 5π 面積 π 半径 xcm, 中心角a°とする
おうぎ形 面積 応用問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
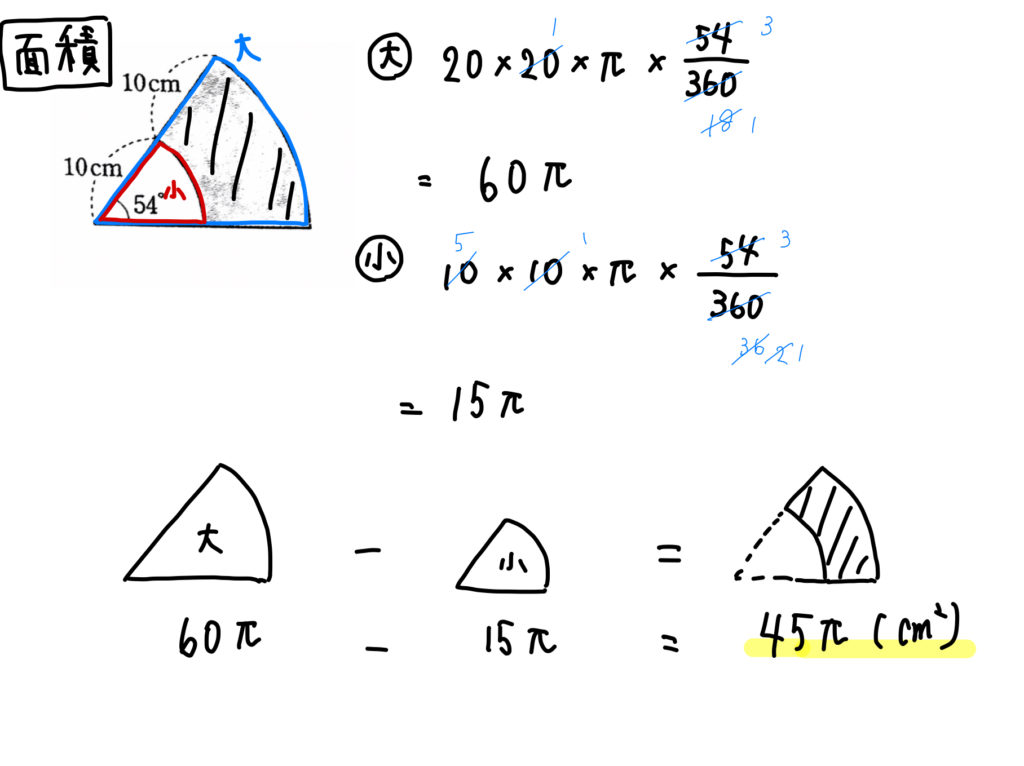 | 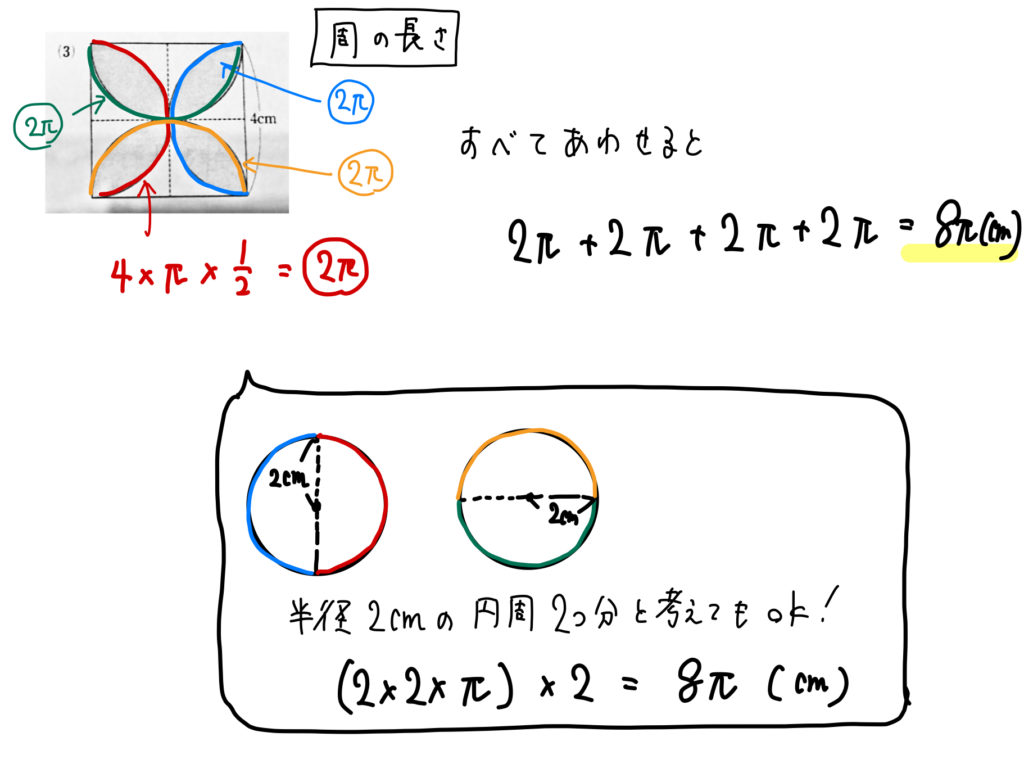 | |
 | 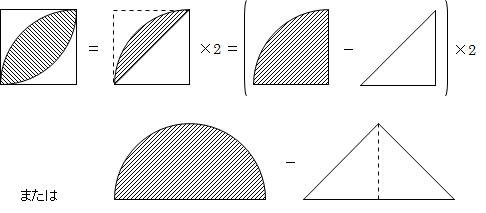 | 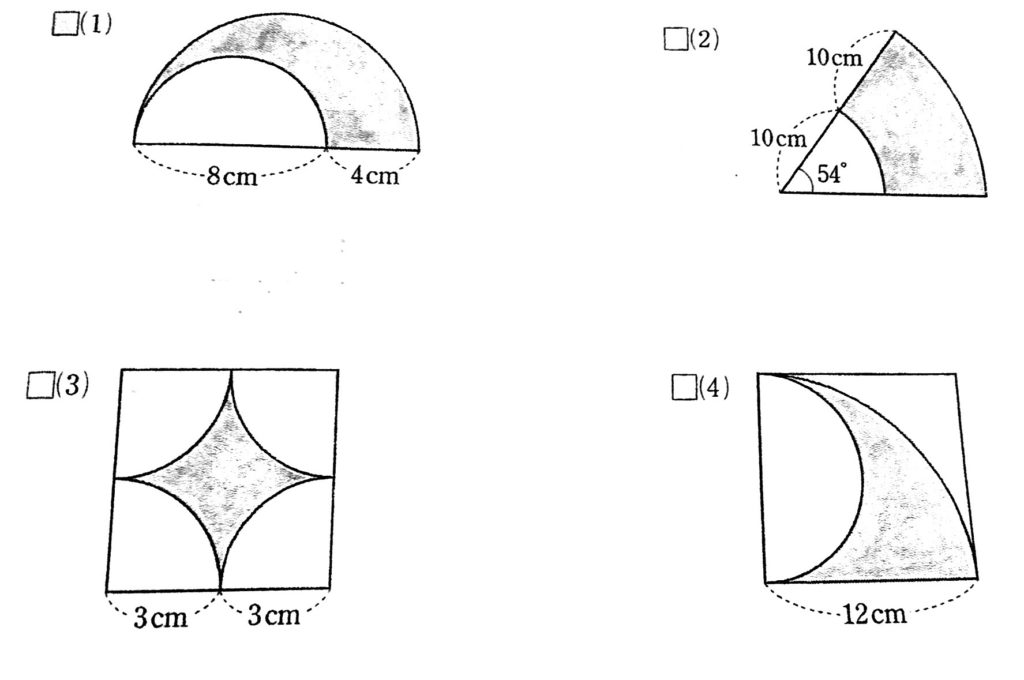 |
 |  | |
 |  |  |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  |  |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  |  |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
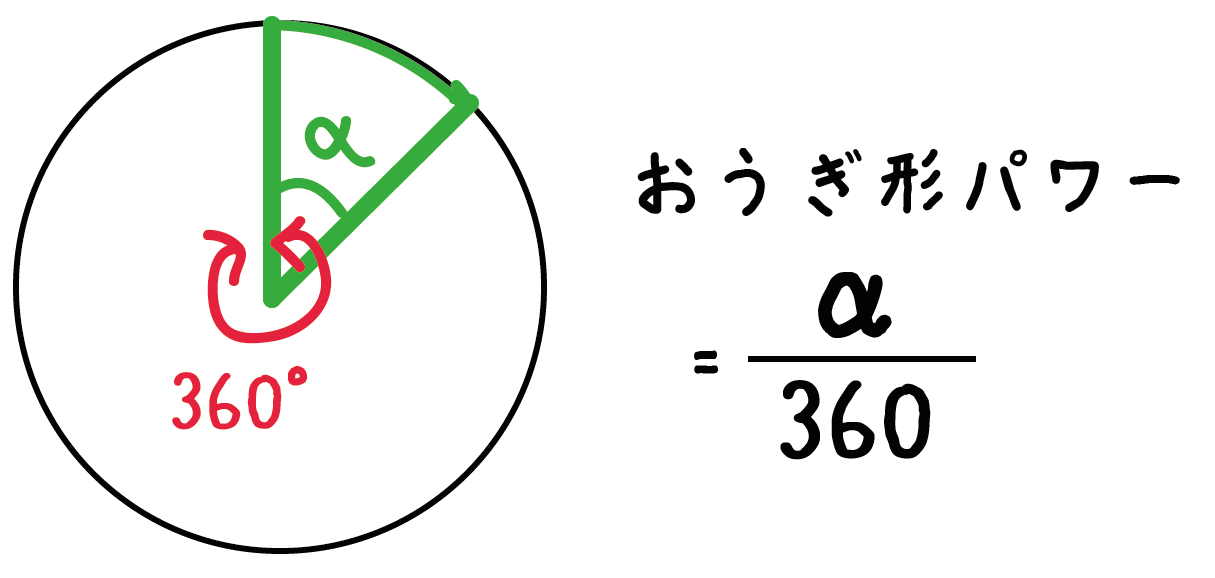 |  | |
 |  |  |
「おうぎ形 面積 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |
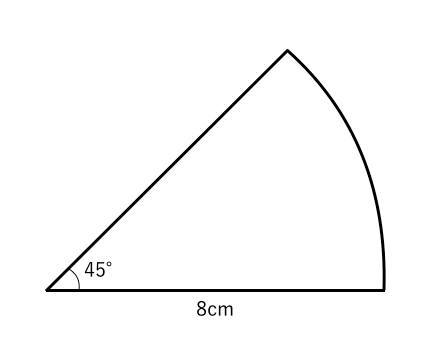
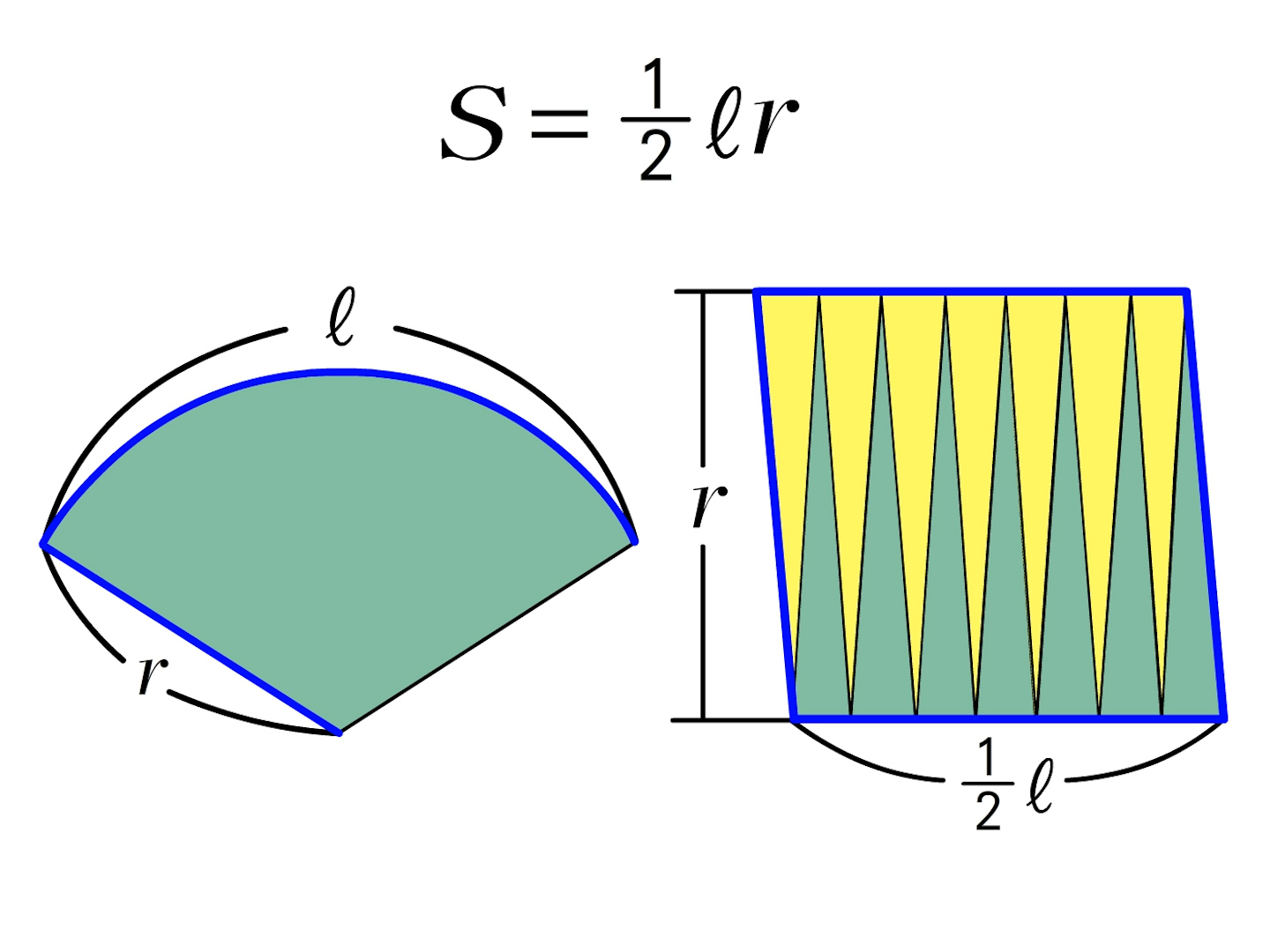
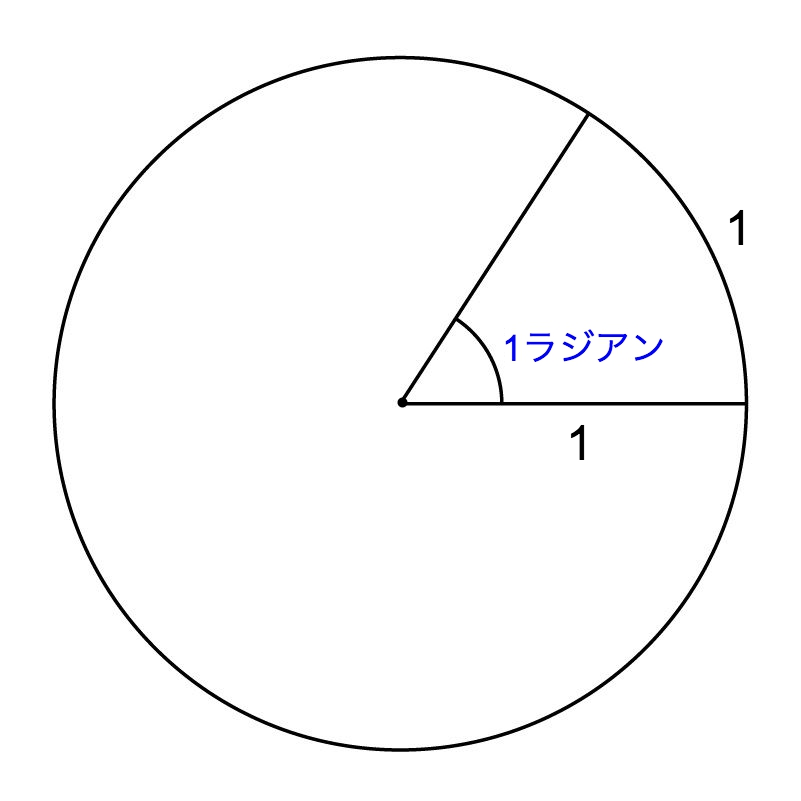
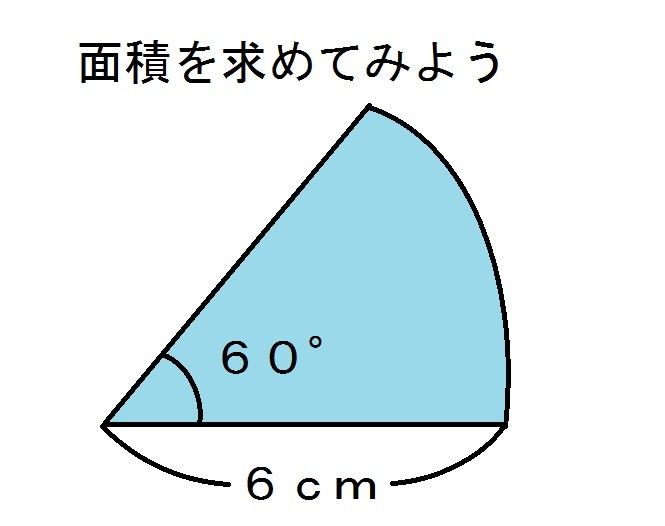
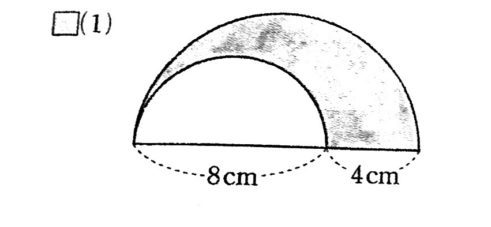
今度は、おうぎ形の面積を考えましょう。 先ほどの弧の長さのときに見た、比を使う方法で考えてみましょう。 半径が r で、中心角が θ のおうぎ形の面積を S とします。 もしおうぎ1 直径8の円の上半分の面積 直径が8だから半径は4.半円だから円の面積の半分:4 2π ÷2=8 π π 採点する やり直す 解説 2 半径 6 ,中心角が1°の扇形の面積 1°だから円(360°)の3分の1 6
Incoming Term: おうぎ形 面積 応用, おうぎ形 面積 応用問題, おうぎ形 面積 応用 求め方, おうぎ形 面積 応用 公式, おうぎ形 面積 応用 中1, おうぎ形 面積 問題 応用, 扇形 面積 応用,



