初中数学 以三角尺为背景的平行线问题 哔哩哔哩 つロ干杯 Bilibili
平行線 の錯角が 証明と合同の性質を使った問題です。 証明問題は嫌われがちですが、本質的に今までの角度や長さを求める問題とあまり変わりません。若教師能提供實物三角尺供學生檢驗平行線，教學效果更佳。 03 三線八角 Angles associated with Parallel Lines 教師可利用課件介紹同位角、內錯角和同旁內角的意義，並透過拖拉非平行線成為平行線，展示有關角度的變化。
平行線 角度
平行線 角度-平行線と角度 平行な線に交わる直線の角度を求めます。 はじめに、対頂角、同位角、錯角を確認しましょう。 対頂角は等しい。 平行線の同位角は等しい。 平行線の錯角は等しい。 図2の x の角度を求めてください。 1． 下の図で、2つの直線が平行で我们要做四步： 一 、看看已知的边是对边、邻边还是斜边。 二 、用上面的公式来决定用 正弦、余弦 或 正切。 三 、正弦：求 对边/斜边，余弦：求 邻边/斜边, 或 正切：求 对边/邻边。 四 、用计算器来求角度，用 sin 1 、cos 1 或 tan 1
初中数学相交线与平行线知识小结 知乎
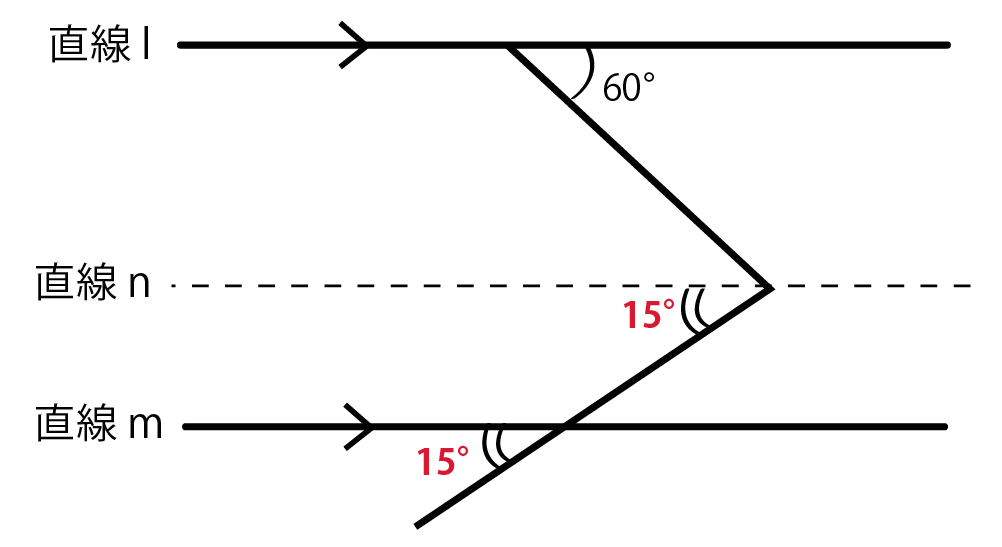
図2のような図形の場合、赤で示した角度は1文字で表せない。 ∠eとしてしまうと青い部分、赤い部分または両方合わせた部分の どれを指すかわからなくなるためである。 このため3文字で∠gefとあらわす。 青い部分は∠deg、両方合わせた部分は∠defである。影片：平行線與橫向線形成的角度 (英)，khan videos > 角與角度。源自於：均一教育平台 願 每個孩子都成為終身學習者，成就自己的未來。同様にして，黄色で示した三角形の内角の和が 180 ° になることから，∠q=130 ° これにより，∠s=50 ° （「黄色の三角形で，外角 ∠s は，それと隣り合わない2つの内角の和 ∠a ∠c に等しい」と考えてもよい．） 右下の三角形の内角の和が 180 ° になる
對於非零向量 ，以 x 軸正向為始邊， 所在射線為終邊所夾的角度 q （ 0 £ q < 2 p ），稱為 的方向角即 。 12 向量的加減與實數積 1 向量加減與實數積的坐標表示法： 設 ， ， r 為實數，則 (1) 。 (2) 。 (3) 。 2 向量的平行： 設 ， ，則 Û a 1 b 2 = a 2 b 1 ；當 b 1 b平行線 在歐幾里得空間中，直線的方向向量是一個單位向量 ，使得原點到直線上所有點的向量都能表示為 , 。 若干個由方向向量,,, 確定的直線相互平行若且唯若這些向量全部相等或只差一個正負號。 在歐幾里得空間中，平面的法向量是一個單位向量 ，使得平面上所有的向量都與 垂直。2 性質 (1) 兩平行線之間的距離處處相等。 (2) 兩平行線永遠不會有交點。 二、截角 1 同位角： 如右圖， 1 在 L1 的右上方， 5 在 L2 的右上方， 像這樣位置關係相同的角就稱為同位角。 同理， 2 和 6 、 3 和 7、 4 和 8 的都是同位角。 2
平行線 角度のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 | 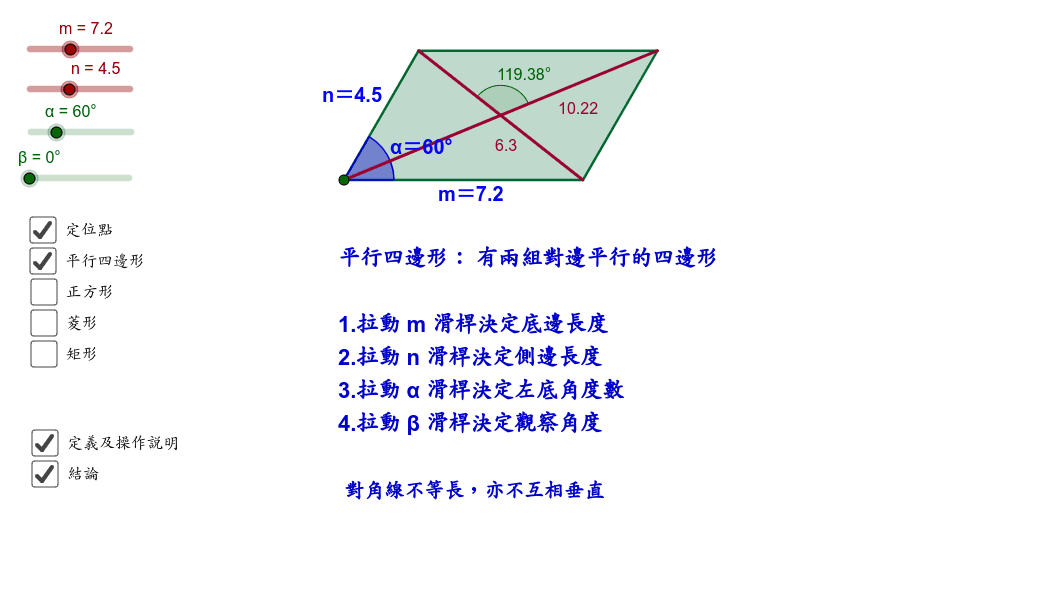 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 | 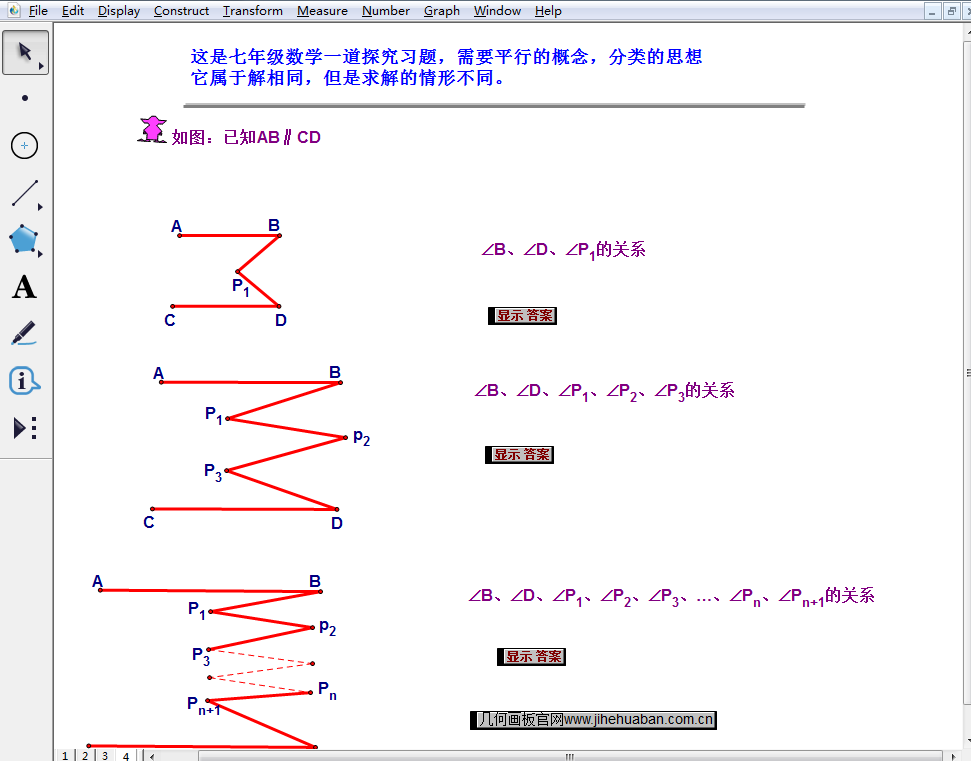平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |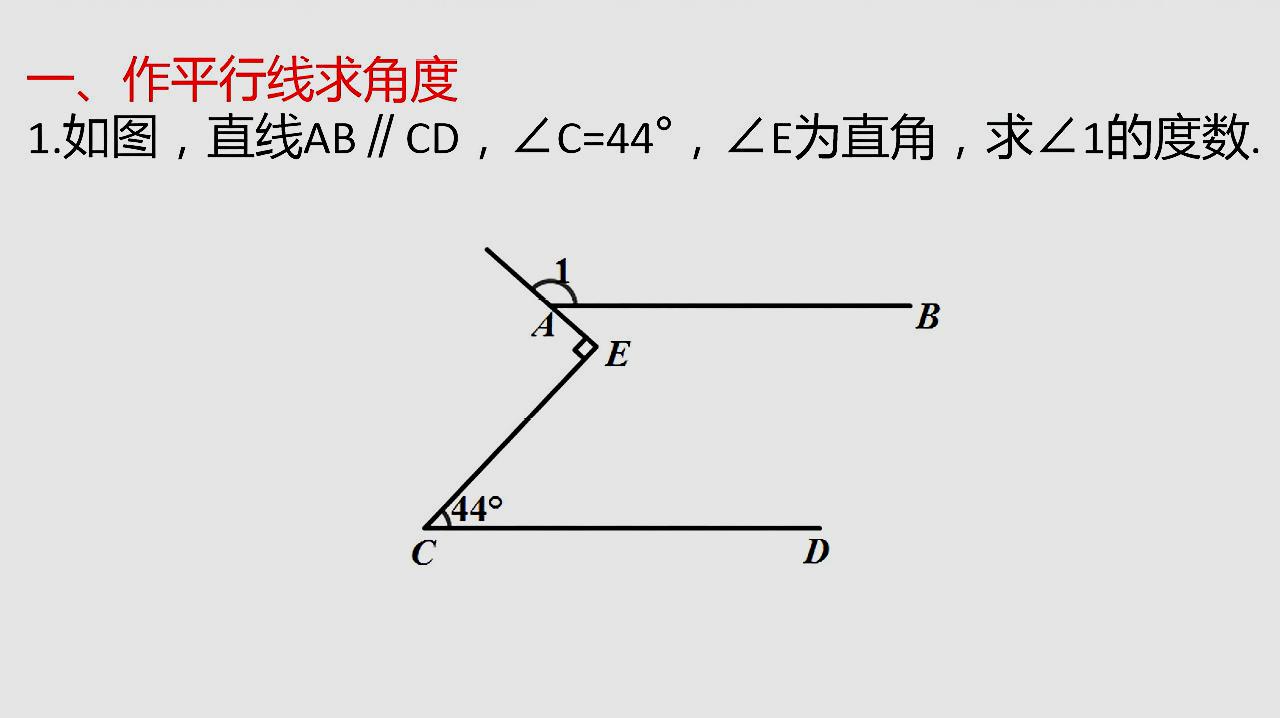
 平行四边形的性质 禾教 初中数学互动课堂 |  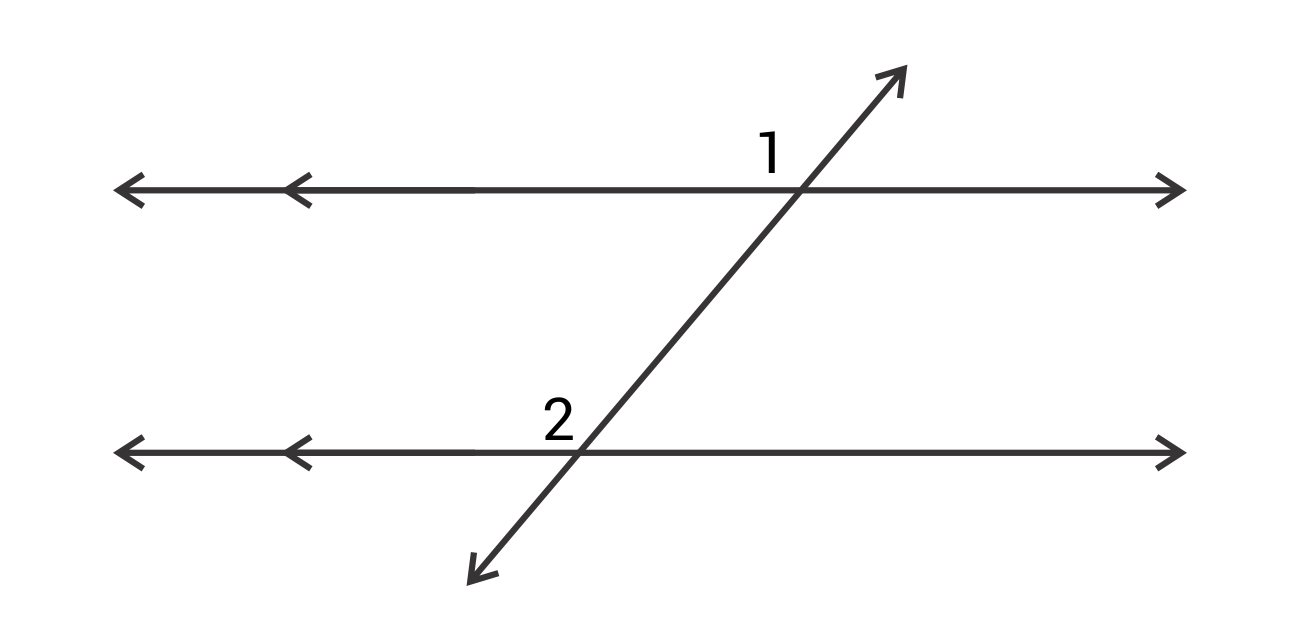平行四边形的性质 禾教 初中数学互动课堂 | 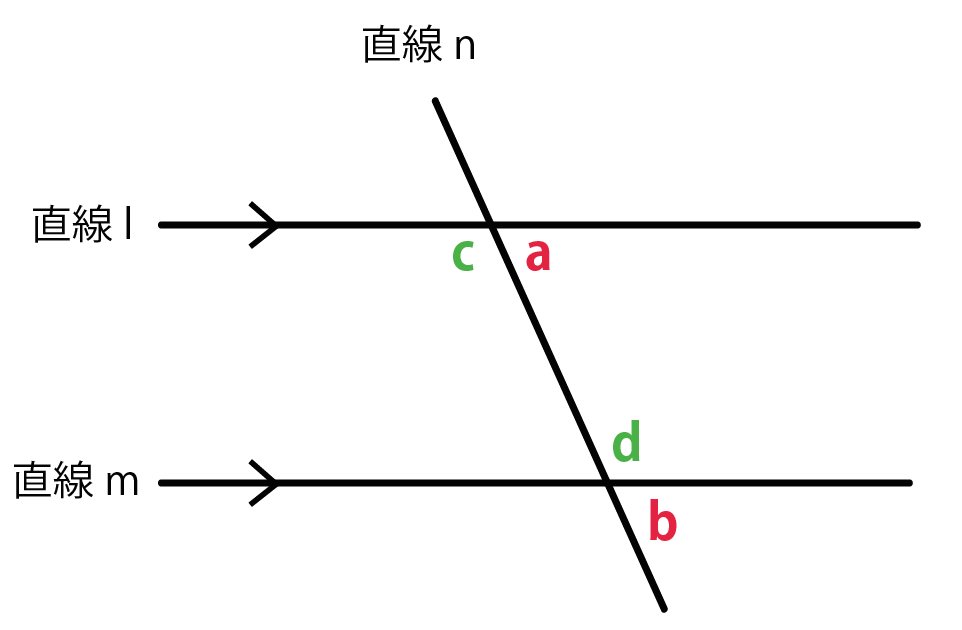 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 | 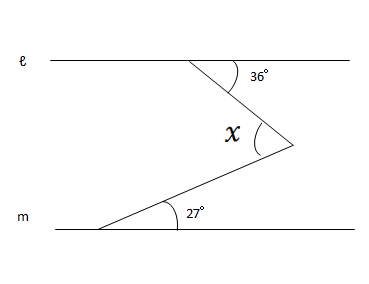 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 | 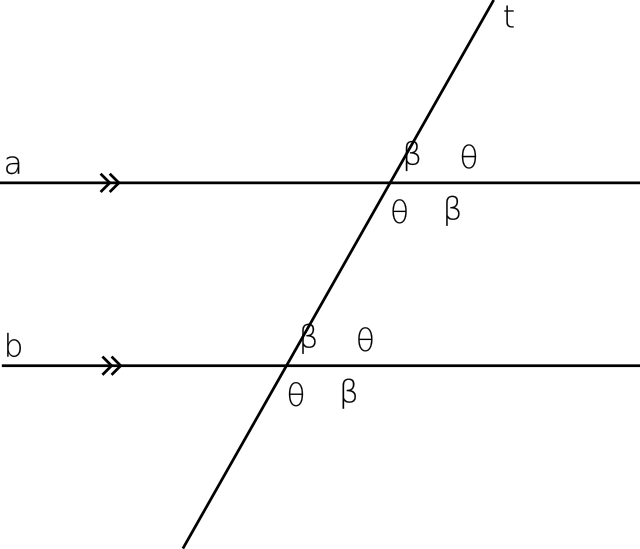 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 | 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 | 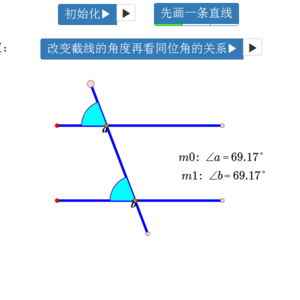 平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
 平行四边形的性质 禾教 初中数学互动课堂 |  平行四边形的性质 禾教 初中数学互动课堂 |
図1のように， ∠A=37°, ∠E=°, ∠CFD=97° の図形がある。 ∠x の大きさを求めなさい。 （北海道17年入試問題） 解説 やり直す ∠x= ° 採点する 4つある三角形について，各自が思いつく順に角度を埋めて行けばよいでしょう （解答） ADE について， ∠D(2) 針金を点Aで固定し、何回か折り曲げて多角形を作るとき、折り曲げる角度を全て 15°にし、頂点Aの一つの外角も15°にするには、何回折り曲げればよいか。 60° 180°×(162)=25 180°×(1)= 180°×(n2)=2340° 180°×(n2)=1800° 360° 360° 十五角形 十二角形 540° 7
